人は迷う。検討に何時間使うのが適正か?
人は迷う。
どの商品を買おう、どこに旅行に行こう。何を食べよう。
今交際している相手と結婚すべきか、もっと良い運命の人が現れるのを待つべきか…
そして、迷っているうちに、最有力候補としていた宿の部屋が埋まってしまったり、食事を取る時間がなくなって昼飯抜きになったりする。
一方、早く決めた場合は、もっと良い選択肢があったのではないかと後悔をする。
悩ましい問題ではあるが、アルゴリズム研究の分野でこの答えは出ている。
検討時間を全体の37%にするという答えが。
世界中の誰しも人生において時間は有限である。
今年何をして何をしないか、今日一日で何をして何をしないか、経験済みの体験をより深堀りするのと未経験の体験をすることのどちらに時間とお金と体力を費やすべきか。
悩んでいる時間は有限な時間の消費ともいえる。これに一つの基準があるのであれば、使ってみることで限りある時間の有効活用ができるのではないでしょうか。
アルゴリズムとは
世間認知としては、NHK教育の「アルゴリズム体操」で知った人が多いかもしれない。ではアルゴリズムとは何かを説明できる人は?となると、意外と少ないのではないでしょうか。
辞書の定義によると、
ある特定の問題を解いたり、課題を解決したりするための計算手順や処理手順のこと。これを図式化したものがフローチャートであり、コンピューターで処理するための具体的な手順を記述したものがプログラムである。イランの数学者・天文学者、アル=フワーリズミーにちなむ。
デジタル大辞泉
問題を解決するための方法や手順のこと。問題解決の手続きを一般化するもので、プログラミングを作成する基礎となる。アルゴリズムは1つの問題に対し、複数ある場合が多い。たとえば、文字をアルファベット順に並べ替えるには、複数のアルゴリズムが考えられる。アルゴリズム次第で、プログラムのサイズや汎用性などが変わってくるため、効率的と思われるものをプログラムに採用する。アルゴリズムは流れ図(フローチャート)を用いて図式化される。
ASCII.jpデジタル用語辞典
アルゴリズムを簡単に言うと、問題を解決するための手順・計算方法です。
ここで考慮する必要があるのは、ある結果にたどり着くための手順(アルゴリズム)はたくさんあるということです。最終的に同じ結果になるのであれば、効率が高く、短時間で計算できるアルゴリズムのほうが優れているわけです。
コンピューター用のアルゴリズムを記載したものがプログラムなので、コンピューター専門の用語と思われがちですが、アルゴリズムは問題を解決するための手順・計算方法なので、汎用性があります。
身近なアルゴリズムとしては、料理が挙げられます。千切りキャベツを作るのに、1枚の葉を文字通り千切りしようとすると途方もない時間がかかるが、葉を重ねて巻いたものを切ることで食感を高めつつ短時間で作れるわけです。また、レシピを見て調理をすること自体が効率よく精度の高い結果を出すためのアルゴリズムに従っているわけです。
そして、数学でいう四則計算のように答えが存在する問題のアルゴリズムは単純ですが、現実の問題にはたった一つの答えなど存在しないことが多いものです。
冒頭で記載したとおり、人は単一の答えのない問題に悩む。どこまで検討すれば正しいのか?
これに数学者は「最適停止問題」という呼称を与えている。
以降、アルゴリズム思考術~問題解決の最強ツール~(Brian Christian & Tom Griffiths)を参考に記載していきます。
最適停止問題として最も著名な秘書問題
前提
一人の優秀な秘書を採用するために、秘書の面接に応募してきた人たちを面接している。面接官はランダムな順番で、一人ずつ面接していく。面接した応募者を採用したいと思ったら、好きなところで採用を決定して良い。選ばれた応募者は辞退しないこととする。その時点で面接は終了する。
ただし、一度不採用として見送った応募者を後から採用することは出来ない。
目標
応募者の中で最も優秀な人材が採用できる可能性を最大化すること
以上、説明はごく簡単な問題だが、解くのはすこぶる難しい。
秘書探しが失敗に終わるのは、決定して終わらせるのが早すぎたか、遅すぎた(最適者を見送った)のいずれかです。
早すぎた場合は、最も優秀な人材には出会わないで終わる。遅すぎた場合には、もっと優秀な人材がいつのではないかと存在しない応募者を待ち続けることとなる。この戦略を最適化するためには、慎重さと軽率さのバランスを取る必要がある。
最も優秀な応募者を見つけようとしていて、一番以外は要らないと思っているなら、今までに面接したなかで最良ではない応募者を採用することなど考えてはならない。…しかし、今までで最良の応募者が現れたとしても、それだけでは採用を決めるに十分ではない。…面接を進めていくにつれて「今までで最良」の応募者に遭遇する確率は当然下がっていく。たとえば二人めの応募者が今までで最良となる確率は半々だが、五人めでは五分の一…最初に出会った「今までで最良」の応募者を採用するのが早計なのはわかりきっている。応募者が100人いる場合、一人めよりも優秀だからという理由で二人めの「今までで最良」の応募者を採用するのはやはり急ぎ過ぎだろう…
最適解は「見てから翔べルール」というものであり、「見る」(選択肢を探ってデータを集める)作業にかける時間を予め決めておき、その間は良さそうな応募者が現れても採用しない。所定の時間を過ぎたら、「跳ぶ」段階に入り、これ以降に「見る」段階で出会った最高の応募者より優れた人材が現れたら、ただちに採用する。
仮に応募者を三人だとする。ランダムに選ぶなら33%で最良の応募者を採用できることになる。ただし、ランダムを上回る方法がある。一人めの面接では情報がない。三人めの面接では後がない。今までの応募者を全て落としてしまったので、最後の一人を採用するしかないから。しかし、二人めの面接では情報もあるし、選択の余地がある。一人めより優秀なら採用し、そうでないなら断ることにしたらどうか。
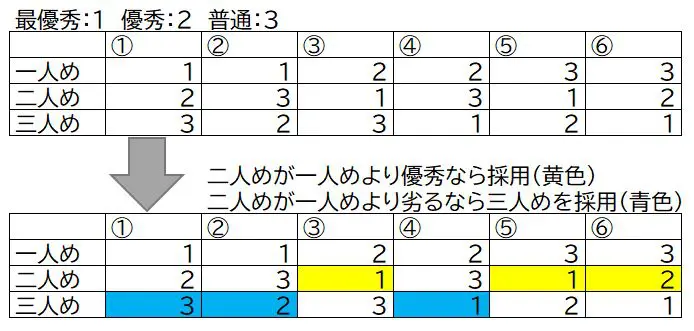
上の表を見れば、一目瞭然ですね。6パターン中3パターンで最も優秀な秘書を雇うことができるのです。
当然応募者が増えると、この基準と採用確率は下がっていきますが、いずれ「見る」段階と「跳ぶ」段階の境界線が37%付近で落ちついてきます。
応募者が5人であれば、採用に入る前に「見る」のは2人(40%)、最良の応募者採用確率は43.33%ですし、
10人であれば「見る」のは3人(30%)、最良の応募者採用確率は39.87%、100人であれば「見る」のは37人(37%)、最良の応募者採用確率は37.1%、
1,000人であれば「見る」のは369人(36.9%)、最良の応募者採用確率は36.81%です。
このモデルの優秀なところは、母数が多くなるほど、ランダム選考に対する優位性が大きくなることです。
例えば、1,000人の応募者からランダムに選んだとすると、最良の応募者である確率は0.1%です。しかく、このアルゴリズムを活用することで36.81%まで高めることができるわけです。
まぁ、現実には秘書採用であれば、全員面接して即時の結果発表を保留して最適者を選考するということになるわけです。
しかし、これが結婚相手ならどうでしょう?
このアルゴリズムの有用性が理解できるのではないでしょうか。
運命の人を求めるあまり独身が続いている人は周りにいませんか?





